【Tokyo Doves】強力な必要条件を駆使して詰み局面を全列挙する

引き続き Tokyo Doves の記事です。板についてきました。今回は詰み局面の全列挙の方法について紹介します。

詰み局面の定義

詰みの定義を考えるために将棋を参考にします。将棋では「自分が何を指しても次に相手が自分の玉を取ることができる状態」を詰みと呼びます。同じように Tokyo Doves での詰みを考えると、「自分が何を指しても次に相手が自分のボスを囲むことができる状態」を詰みと定義するとよさそうです。以前の記事で議論したように1手で自滅しない手が存在するので、そのような手のうちどれを選んだとしても、その後相手が自分のボスハトを包囲するような手がある、という風に考えればよさそうです*1。この記事ではこの定義を Tokyo Doves での詰みとしておきます。

探索の方針

詰み局面を全列挙するには、詰み局面の可能性のあるものをすべて探索する必要があります。しかしルール上可能な局面は 通りぐらいあるので、これを全部確かめていたのでは日が暮れるどころか人類が滅びてしまいます*2。そこで局面数を数えたときと同様に、ハトの配置の形と、具体的にどの種類をどこに割り当てるかを分けて考えてみることにします。前回の記事をまだ読んでない方は読んでみてください↓
smooth-pudding.hatenablog.com
前回は、ハトの割り当て方の部分が理論的に計算できるので、全体の数え上げも一瞬で終わるという構図をしていました。つまりハトの配置の形自体の種類は大したことないということです。今回も割り当てのところを手軽にできる方法を考えます。(ハトの配置の形の列挙に関しては前回から新しいことは特にないので省略します)

ハト配置の形状が与えられたときの詰み局面の全列挙

前回同様、今回も理論的に片付けてハイ終わり・・・というわけにはいきません。今回はどのようにハトを置いたら詰み局面なのかをすべて列挙する必要があるので、実際に並べてみる必要があります。これは避けられない現実ですが、なるべく工夫して、並べる前から絶対に詰み局面ではないものを省いてみます。
まず、ハトを並べた時点で相手や自分のボスハトが包囲されているような局面は対象外です。詰み判定をする前にゲームが終了しているからです。なので、ハトを並べるときは、自分と相手のボスハトがいずれも包囲されていないような場所に置くことだけ考えればよいです。形状からどの位置が包囲される場所かは特定できます。例えば

x	x		x
	x	x	x
	x	x	x
		x	x

上記のような形状が与えられたとして、包囲されている場所を o に置き換えると

x	x		x
	x	x	o
	x	o	o
		x	o

となります。互いのボスハトは o 以外の場所に配置し、そのあとに残りのハトをどこに並べるかを考えれば良いことになります。
しかしこれだけでは焼け石に水で、抜本的に計算時間が劇的に短くなることはありません。やはり人類が滅びてしまいます。実は人類の滅亡を防ぐ方法、いえ人類が滅亡する前に詰み局面を全列挙するための妙案があります。その説明をするために、包囲度という概念を導入しておきます。

包囲度

盤面上にある特定のハトに対し、その包囲度は、そのハトの四方のうち、ハトがいたり壁があったりするのは何個あるか、という量として定義しします。例えば

x	a
x			x
	x	x
x

以上の x の各位置にハトがいるとき、a のハトの包囲度は 2 となります。a の左隣にハトがいるのに加えて、上側は壁ができており、合わせて2方向が包囲されている、と数えます。もし

x	a
x			x
	x	x
x

のように a の上側が壁でなければ、a の包囲度は1となります。
包囲度の言葉を使えば、自分が負ける条件は、自分のボスハトの包囲度が4となること、と表現できます。相手のボスハトの包囲度を4にしたら勝ち、とも表現できます。

詰み局面となるための必要条件

元の話題に戻ります。ハト配置の形状が与えられたとき、ハトを並べまくっていると時間が掛かりすぎるという話でした。実はハト配置の形状と自分のボスハトの位置のみから、即座に詰み局面となりえないと判断しうる性質があります。それが以下です。

ハトの配置の形状が与えられ、そのうち自分のボスハトの位置が確定しているとする。もし自分のボスハトを (合法的に) 動かした結果、ボスハトの包囲度が2以下になるような手があるならば、他のハトをどのように配置したとしても、詰み局面とはならない。

何言ってるか分からない人も多いと思うので、具体的に説明します。

x
	x	x	B
x	x	x	x
x	x	x	x

以上のように自分のボスハト B となんらかのハト x 11羽が配置されている場合を考えます。それぞれの x にどのハトが並ぶかは現時点では未定です。B が合法的に動ける方向は上方向または斜め上方向です(ボスハトをどう動かせるかについては x にどうハトが並ぶかに関係ありません)。例えば上方向に動かすと

x			B
	x	x
x	x	x	x
x	x	x	x

となります。このときの自分のボスハトの包囲度は2です。動かした結果包囲度が2となるようなボスハトの動かし方がある、すなわち先ほどの性質の仮定を満たします。すると、現時点でまだ x にハトを並べていないにも関わらず、元の形状は絶対に詰み局面ではないことが判明してしまいます。
理解のために詰み局面が起こりうる形状についても考えてみます。例えば以下の配置はハトの並べ方によっては詰み局面となります。

	x		B
		x
		x	x
x	x

ボスハトの合法的な動かし方は、左方向か下方向の2通りがあります。左方向に動かすと

	x	B
		x
		x	x
x	x

となり、ボスハトの包囲度は3です。下方向に動かすと

	x
		x	B
		x	x
x	x

となり、やはりボスハトの包囲度は3です。先ほどの性質の仮定を満たさないので、具体的に並べてみないと詰み局面があるかどうか分かりません。ちなみにどのように配置すると詰むかというと例えば

	b		B
		x
		c	d
x	x

(b: 相手のボスハト, c: 相手のハジケハト, d: 相手のアニキハト, x: 残りの相手のハトいずれか)
が具体例になります。ボスハトが左や下に動くと即座にハジケハトが飛んできて敗北しますし、持っているハトをボスハトの隣に配置すると相手のボスハトやアニキハトが寄ってきてやはり敗北します。他に指せる手はないので、まさしく詰み局面です。
この性質の証明は後に行うとして、この性質が成り立っていることのありがたみを考えてみます。この性質は、一つひとつハトを並べずとも、ボスハトの動かし方を検査するだけで、ハト配置の形状をボツにできる可能性があると主張しています*3。与えられた形状に対してざっくりハトの欄の階乗ぐらい探索パターンがあることを考えれば、この方法でボツにできるだけでかなり強力そうであることが想像できるのではないかと思います。

詰みのための必要条件の証明

さて、前節で紹介した性質を証明していきます。証明は2ステップで実行します。

事実1: 相手のボスハトの包囲度を2以上上げる手は特殊な例外のみ

1手で相手のボスハトの包囲度をなるべく上げる方法を考えます。包囲度を上げるには、

• 相手のボスハトの上下左右隣にハトを移動させる
• 相手のボスハトの上下左右隣に壁を作る

のいずれかしかありません。このうち前者で包囲度を2上げることは不可能です。相手のボスハトの上下左右に新たにハトを2羽増やそうにも、動かせるのは1羽のみだからです。また前者と後者を組み合わせて包囲度を上げる方法もありません。ボスハトのすぐ隣に壁を作るには、ボスハトが接している方から反対側の壁にハトを移動させるか配置するかする必要があります。当然このハトは相手のボスハトに隣接しないので、ボスハトの隣にいるハトの数は変わりません。
したがって、相手のボスハトの包囲度を2以上上げるには、新たに2つ以上の壁をボスハトの上下左右のいずれかに作るしかありません。2つ以上と言いましたが、ひとつのハトが接することのできる壁は最大2つであり、4x4 の隅にいるパターンしかありません。よって、1手でボスハトの包囲度を上げる最大幅は2であり、2上げるには

B			x
			x
			x
x	x	x	o

上記の x, o の位置には元々ハトは一切おらず、1手によって o の位置にハトが移動するか手札から置かれるというパターンしかありません*4。それ以外のパターンだと包囲度は高々1しか上がりません。

事実2: 特殊な例外のケースは詰み局面を生まない

事実1の議論から、特殊な例外ケースを除いてボスハトの包囲度は1手で1までしか上がらないことが分かりました。このことから、もし自分のボスハトの包囲度が2以下の状態で相手の手番となった場合、特殊な例外ケースのパターンになっていない限りは、相手の1手で自分が敗北することはないと分かります。そこでここでは警戒すべき特殊な例外について考えてみます。例外ケースで次の相手の1手で自分が敗北するかもしれない局面は、以下の形になります。

B	①	②
③	④	⑤
⑥	⑦	⑧

相手の手番で⑧の右下が新たに埋まったタイミングで自分のボスハトの包囲度が4になるには、①と③が既に埋まっている必要があります。この配置の一手前について考えてみます。元々示したかった性質のことを思い出しておけば、自分の手番でボスハトを動かしてこの位置にやってきた場合のみ考えれば十分でしょう。
①, ③が埋まっていることを前提とすると、一手前は次のパターンのみを考えれば十分です*5。
(1)

B		①	②
	③	④	⑤
	⑥	⑦	⑧

(2)

		①	②
B	③	④	⑤
	⑥	⑦	⑧

(3)

	①	②
③	B	⑤
⑥	⑦	⑧

(1) や (2) のパターンのときはそれぞれ (2) や (1) に動かす手が合法で、いずれもボスハトの包囲度が2以下の1手で敗北し得ないパターン (=特殊な例外でないパターン) です。すなわち (1) や (2) は詰み局面ではありません。(3) の場合、⑤か⑦のいずれか一方は空欄である必要があり (そうでなければ既にゲームが終了している局面なので不適)、そちらの方向にボスハトを動かすとやはりボスハトの包囲度が2以下の1手で敗北しえないパターン (=特殊な例外でないパターン) となります。すなわち (3) は詰み局面ではありません。
以上の議論から、特殊な例外パターンからは詰み局面は生まれないことが分かりました*6。これにより晴れてボスハトを動かした結果包囲度が2以下となる手があるなら、詰み局面でないことが示されました。

全列挙の結果

ここまで紹介してきた手法とビットボードを使った高速な実装、また Rust コンパイラによる最適化を経ることで、現実的な時間 (たしか数日程度？) で全列挙することができました。ちょっと漏れがある疑惑が最近出てきているので正確な数値かどうかは若干怪しいのですが、平行移動・反転・回転で一致するものを除いた上で、詰み局面は全部で

通り 通り
ありました。*7(追記 (2022/11/12): 追試したら以下になりました:
通り
より詳しく、フィールド上にいるハトの数に対応する局面数、および合計の局面数は以下のとおりになりました。)

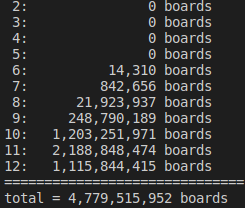
次回以降、ここから出発した後退解析について紹介できるといいなぁと思っています。(が、まだ試行錯誤しながら探索中なのでいつになることやら・・・)

*1:細かいことを言えば同時にボスハトが囲まれてしまう手をどうするか問題があるのですが(ルールについて考えてみる回参照)、今回の記事の内容は(最後の局面数を除いて)そのときの裁定をどのように決めても正しいはずです。

*2:実は人類は滅びないかもしれませんが、数ヶ月とかかかりそうぐらいにはなります。

*3:正確には、形状とボスの配置の組み合わせをボツにするということです。同じ形状でも、あるボスハトの位置ならボツだが、別のボスハトの位置なら耐え、という状況はあり得ます。

*4:ここでは空欄は未定の意味であり、ハトがいないことは意味しません。

*5:左斜め上から来る手はボスハトが孤立しているので非合法。上や右斜め上は対称性から (2) や (3) で事足りる。

*6:より証明の内容に即した丹念な表現をすると、もし仮にボスハトをある方向に動かした結果の局面が例外パターン(包囲度が2で壁同時生成により包囲度4になる)に該当するとしても、別の方向に動かすことで包囲度が2以下の例外パターンでない状況を作れる、ということです。

*7:ここでは、自分の手の結果両者のボスハトが同時に囲まれた場合、自分が敗北するというルールを採用しました。

【Tokyo Doves】実現可能局面数をざっくり見積もってみる

引き続き Tokyo Doves のシリーズです。今回は Tokyo Doves の実現可能局面数について見積もってみます。

実現可能局面数とは？

実現可能局面数とは、実際にゲームの進行で実現しうる盤面の状態すべての数です。参考までに他のボードゲームの実現可能局面数の概数を列挙すると

• ○×ゲーム:
• チェッカー:
• (8x8)オセロ:
• 将棋: (?)
• 囲碁: (?)
• どうぶつ将棋:

ぐらいらしいです。ちょっと自分で調べるのをサボって以下の動画から数字をコピペしました(なので正確に知りたい方はご自分で文献を探してください)。この動画はどうぶつ将棋の解析について紹介しています。
www.youtube.com
実現可能局面数の大きさの多寡によって、そのボードゲームを完全攻略するための難易度をおおよそ見積もることができます。例えば通常の 8x8 オセロは未だ完全解析されていないそうですが、6x6オセロは既に完全解析が完了しています(4目差の後手必勝)。6x6オセロの実現可能局面数はおよそ だそうなので*1、この付近がギリギリ頑張れるラインかな、と考えることができます。

超ざっくり見積もり

まずはあまり難しいことを考えず、どんぶり勘定で数えてみます。Tokyo Doves は4x4の範囲に入るように常に進行するので、各ハトの位置はそれぞれ4x4の16個のマス目のどこかに位置すると考えることができます↓

x	x	x	x
x	x	x	x
x	x	x	x
x	x	x	x

赤組のボスハトと緑組のボスハトは常に盤面上にあります。これらの配置の仕方は 通りあります。それ以外のハトは両組合わせて10羽いて、そのうち0羽以上10羽以下が盤面に配置されます。配置されるハトの数を 羽とすると、配置されるハトの選び方が 通り、これらのハトの配置の仕方が 通りとなります。以上を足し合わせると

となります。値は Python の以下のコードで計算しました。答えは一瞬で出ます。

from math import comb, perm
print(sum(perm(16, 2) * comb(10, k) * perm(14, k) for k in range(11)))

超ざっくりならこれでいいのですが、ルール上同じ局面を複数回数えている部分があります。例えば x, y, z をなんらかのハトとするとき

x	z
		y
			x
			x

と

x
	x	z
			y
x

はルール上同じ配置ですが、この数え方だとそれぞれ別の局面として数えています。また

x	z
		y
			x
			x

と

x
z
	y
		x	x

と

		x	x
	y
z
x

はパッと見違う形ですが、相対的な位置関係は同じなので、事実上同じ局面と言って良いでしょう。つまり回転・反転によって同じ形になるもの同士は同じ局面として数えるのが自然です。またハトが孤立するようなパターンの排除したいです。こうなると、もはや簡単な計算式では対処できません。そこでもうすこしガッツリプログラミングを使って数えてみます。

作戦

通りをすべて検査して重複を取り除いたり孤立するものを取り除いたりしてもよいのですが、かなり時間がかかってしまうので、ここでは別の作戦を取ってみます。具体的には

• 4x4 のマス目のうちハトを配置するマスはどれか
• ↑のマスにどのようにハトを配置するか

の二段階に分けて考えることにします。前者と比べると後者はシンプルな数え上げで、かなりの部分を数式で処理できます。その分前者の数え上げの総量が抑制されて、楽に答えを得られる、という寸法です。

ハトの置き場所が与えられたときにハトをどう配置するかの総量

具体例から考えましょう。以下のような配置場所が指定されたとします。

x	x		x
		x
	x		x
		x

x がハトを配置するべき場所です。xに順に配置していくのですが、その順序は先ほどと同様「両軍のボスハトを配置する→それ以外のハトを配置する」で行います。ボスハトが 通り、残りのハトは5羽で 通りとなります。
次に以下のような配置場所の場合はどうでしょう。

x
		x
	x		x
		x

同じ考えで数えると 通りと言いたくなるところですが、今回は配置場所の対称性があるため、これだと数えすぎになってしまいます。回転・反転で一致するものは同じ局面とみなす、と言ったのですが、今回は回転・反転をどのようにしても形状が変わりません。回転・反転で作られる数は8通り(度回転を4回+反転で2つ)あるので、全てのパターンで8回重複して数えていることになります。なのでこの配置での局面数は 通りとなります。
もうひとつぐらい具体例を挙げておきます。

x
x
	x	x	x
		x

こちらの配置だと反転で一致するのみなので、先ほどの例では8で割っているところを2に変えればOKです。つまり 通りとなります。
以上から、ハトの配置場所とその対称性が与えられれば、一つひとつ列挙しなくても、数式でハトの配置が何通りあるかを数えることができます。いえ、より正確には、(配置するハトの数, 配置の対称性) のペアが与えられれば十分です。

ハトの置き場所の列挙

重複しないハトの配置場所とその対称性を数え上げればあとは簡単、ということが分かりました。そこでここから頑張って配置全体を列挙する方法を考えていきます。
まず16マスに以下のように数字を付けます。

15	14	13	12
11	10	9	8
7	6	5	4
3	2	1	0

そして数字の組み合わせによって配置場所を表現することにします。例えば前章で出てきた配置場所の例なら {1, 4, 6, 9, 12, 14, 15}, {1, 4, 6, 9}, {1, 4, 5, 9} になります。こうすることによって、0~15の16個の数字からいくつか取り出す組み合わせ全体を総当りで調べれば終わることが分かります。この総当りは

通りなので、コンピュータなら一瞬でできそうです。
あとは平行移動・回転・反転で一致するものを取り除くこと、孤立ハトがあるものを取り除くこと、対称性を数えることです。これを実装するためにビットボードというものを考えます。

ビットボード

ボードゲームの状態をビット列で表現して、ビット演算でボードゲームを管理する、という手法があります。このようなビット列で表したボードをビットボードと呼ぶようです。以下のサイトではオセロをビットボードとして実装する方法を丁寧に紹介しています。
zenn.dev

ビットボードを使ってハトの位置のパターンを数え上げることを考えます。16個の位置に「ある」か「ない」かの2つの値をもたせたいので、16bitのデータを考えればよいでしょう。例えば Rust では u16 という型で表現できます。以下は Rust での実装例です。

// 可視化用
fn u16_to_square(x: u16) -> String {
    let flat = format!("{:0>16b}", x);
    let mut chars = flat.chars();
    let mut lines = Vec::with_capacity(4);
    for _ in 0..4 {
        let line: String = (&mut chars).take(4).collect();
        lines.push(line);
    }
    let square = lines.join("\n");
    square
}

// 可視化用
fn print_u16_in_square(x: u16) {
    println!("{}", u16_to_square(x));
}

fn main() {
    let v = vec![1, 4, 6, 9, 12, 14, 15];
    let mut board = 0_u16;
    for x in v {
        board |= 1 << x;  // 番号のところに bit が立った数字を記録
    }
    print_u16_in_square(board);
}

上記を実行すると以下が標準出力されます:

1101
0010
0101
0010

上下左右に1マスシフトするような関数も定義しておきます。この関数は「平行移動すると同じパターン」といったものを省くのに使えます。

fn shift_n(x: u16) -> u16 {
  // 上に1マス
  x << 4
}

fn shift_s(x: u16) -> u16 {
  // 下に1マス
  x >> 4
}

fn shift_w(x: u16) -> u16 {
  // 左に1マス
  (x & 0x7777_u16) << 1
}

fn shift_e(x: u16) -> u16 {
  // 右に1マス
  (x & 0xeeee_u16) >> 1
}

<< や >> はシフト演算子とよばれるもので、ビット列を右辺の数だけシフトする演算です。シフトしてできる余白は0で埋められます。上下方向のシフトは単純に4bit分のシフトとして表現できます。左右に関しては少しだけ工夫が必要です。例えば左方向への1シフトの実装を単に x << 1 としてしまうと、元から左端にあったものが右側からぴょこっと現れてしまいます。これを防ぐためには、シフトの前に

0111
0111
0111
0111

という u16 の数字と bit ごとの and を取ってしまって、その後シフトすればうまくいきます。0111 は十六進法で表すと7なので、この数値は 0x7777_u16 と表現することができます。同様に右方向へのシフトは

1110
1110
1110
1110

をあらかじめ and しておいてからシフトすればうまくいきます。こちらは十六進法なら eeee なので Rust での表記は 0xeeee_u16 となります。
これらの関数を駆使して、可能な限り右下に寄せる関数を定義してみます。つまり右側に余白があれば右に寄せ、下側に余白があれば下に寄せるという操作を可能な限り行います。Rust は当然再帰的な関数をサポートしているので、例えば以下のような書き方ができます。

fn limit_shift_se(x: u16) -> u16 {
  if x == 0 {
    0
  } else if x & 0x1111_u16 == 0 { // 右側に余白あり
    limit_shift_se(shift_e(x))
  } else if x & 0x000f_u16 == 0 { // 下側に余白あり
    limit_shift_se(shift_s(x))
  } else {
    x
  }
}

次に反転と回転ですが、これはビットボードを使わないほうが簡単に実装できます。例えば {1, 4, 6, 9, 12, 14, 15} のボードは

x	x		x
		x
	x		x
		x

で、これの転置形である

x
x		x
	x		x
x		x

は {1, 3, 4, 6, 9, 11, 15} に対応します。このとき転置前の位置と転置後の位置の対応関係を考えておけば、前者から後者を得るための写像が求まります。具体的には

となります。この対応を追えるなら、他のマスも同様に対応関係を決められることも分かりますね。
反転・回転は合計で8種類あるので、この対応関係を与える配列を定数として持っておきます。またこの対応関係を使って Vec を変換する関数も準備しておきます。

const MAP: [[usize; 16]; 8] = [
    [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
    [3, 2, 1, 0, 7, 6, 5, 4, 11, 10, 9, 8, 15, 14, 13, 12],
    [0, 4, 8, 12, 1, 5, 9, 13, 2, 6, 10, 14, 3, 7, 11, 15],
    [12, 8, 4, 0, 13, 9, 5, 1, 14, 10, 6, 2, 15, 11, 7, 3],
    [3, 7, 11, 15, 2, 6, 10, 14, 1, 5, 9, 13, 0, 4, 8, 12],
    [15, 11, 7, 3, 14, 10, 6, 2, 13, 9, 5, 1, 12, 8, 4, 0],
    [12, 13, 14, 15, 8, 9, 10, 11, 4, 5, 6, 7, 0, 1, 2, 3],
    [15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0],
];

fn get_congruents(x: &Vec<usize>) -> [Vec<usize>; 8] {
  let mut cons: [Vec<usize>; 8] = Default::default();
  for elem in x.iter() {
    for (i, map) in MAP.iter().enumerate() {
      let new_elem = *map[*elem];
      cons[i].push(new_elem);
    }
  }
  cons
}

最後にハトが孤立するかどうかの判定について考えます。各ハトの周りを見て、一羽もいないやつがいなければだめ、となるわけですが、ビットボードを使えばかなり効率よく判定することができます。言葉で説明するよりコードを読んだほうが早そうなので、まずコードをご覧ください。

fn is_isolated(x: u16) -> bool {
  let x_n = shift_n(x);
  let x_s = shift_s(x);
  let x_w = shift_w(x);
  let x_e = shift_e(x);
  let x_nw = shift_n(x_w);
  let x_ne = shift_n(x_e);
  let x_sw = shift_s(x_w);
  let x_se = shift_s(x_e);
  let surroundings = x_n | x_s | x_w | x_e | x_nw | x_ne | x_sw | x_se;
  (x & surroundings) != x
}

コードに出てくる x_* はいずれも元のビットボードを8方向のいずれかに移動させたものです。これらの or をとったものが surroundings です。もしハトの位置が surroundings で 1 となっているマスにいれば、それはすなわち他のいずれかのハトが周りにいることを表します。逆に surroundings で 0 となっているマスにいるとしたら、周りに他のハトがいないため孤立することを表します。ということは「孤立している」の必要十分条件は「x と surroundings の and が x から欠損する」となるので、上記のような実装になる、というわけです。
ビットボードでなければ、ひとつひとつハトを取り出して処理して・・・となるところが、ビットボードでは見かけ上並列計算っぽい処理になりました。こういった場面があるため、ビットボードで実装しておくと計算効率の点でメリットを享受しやすいです。

改めて列挙の戦略

ここまでで道具は揃いました。これらを使ってハトの置き場所全体を列挙する流れを整理します。

(1) 0~15 から n 個 (2≦n≦12) の組み合わせを全列挙
... Rust では例えば itertools というクレート*2を使って実現できます。
(2) 各組み合わせに対して、その反転・回転で作られる8つを作る
(3) 8つをそれぞれ u16 のボードに変換し、右下に寄せるように平行移動する
(4) ハトが孤立するパターンであれば棄却し、(1) の次の組み合わせに進む。
(5) 孤立しないことが分かったら、(3) で作ったボードを全て記録しておく
... Rust なら HashSet などを使えばいいでしょう。
(6) 今回作ったボードが新しく記録されたものであれば (つまり (5) の直前に未登録状態なら)、 有効な新しいパターンなので、対応する組み合わせの数を加算する
... 8つのボードで何個ずつ重複するかが「対称性」に対応します。ハトの数は n と分かっているので、このパターンで何通り数えればよいか求まります。

以上をコードに落とし込めば数え上げは完了です！

結果

そして完成したコードがこちら・・・とすればいいんですが、ちょっと人に見せられるようなコードが手元にないので、結果だけ記しておきます。以上の計算を実行すると、求まる局面数は

となります。最初の超ざっくり評価より1桁ぐらい落ちました。計算は一瞬で終わります。
ちなみに、前回の記事*3で紹介したように、

• 両方同時囲いは直前に指したほうが負け
• 履歴による千日手禁止ルールは無し

というルールの下では、両者が最善手を指したとすると、両方のボスが囲まれている状態は実現しません。さらに相手の手番で指した結果、相手のボスが囲まれているという状況も起こりません。したがって、いずれのボスも囲まれていないか、自分のボスのみが囲まれているものが事実上実現されうる局面と考えてもいいでしょう。この条件の下で数え上げると、

となりました*4。これらが全て実現可能かはまだわかりませんが、ざっくりと ぐらいなんだな〜と思えば大きくは外さないようです。

まとめ

全局面数を数え上げるために、本当に全てのものを数え上げるのではなく、ハトの配置パターンとそのときの数え上げを分離し、後者を理論的に計算することで、計算量を大きく下げるようにしました。配置パターンを列挙する際はビットボードというものを使い、シフト演算子や and を有効活用していきました。特にハトが孤立するかどうかの判定では、ビットボードならではの効率化も見えました。
結果として局面数はざっくり ぐらいになりました。完全解析されている 6x6 オセロと比べても悪くない数字で、それなりに解析も不可能ではないと感じさせる結果となりました。次回以降ではより本格的な探索の情報について書いて行けるといいなぁと思っています。

*1:ソースは wikipedia です(ソースと言えないやつ) コンピュータオセロ - Wikipedia

*2:itertools - Rust

*3:【Tokyo Doves】自滅しない手が常に存在することの証明 - ぷりんの雑記帳

*4:囲まれているかどうかの処理は少し工夫が必要です。ビットボードで頑張るなら、ボスハトの上下左右の4マスだけが1になっているビットボードを作って、元のボードの not と and を取れば基本は大丈夫です。ただこれだと 4x4 の壁の有無の処理が足りないので、もう少し頑張る必要があります。ちょっと書くのが面倒なので、読者の演習問題とします(=丸投げ)。

【Tokyo Doves】自滅しない手が常に存在することの証明

あいかわらず Tokyo Doves の解析にドハマりしているぷりんです。
ゲームの進行について考察していると、以下の性質に気づきました。

手番で実行可能な手のうち、自滅しないものが必ず存在する。
(※千日手禁止ルール*1を採用しない場合)

ここで「自滅する手」とは、その手を指すことで相手の手番に移る前に自分のボスハトが囲まれた状態になることを指します。
この記事ではこの性質について証明していきます。

自滅する手

あなたの手番で、以下のような盤面を考えます。

B	x
x		x
	x

ここで B はあなたのボスハト、x はなんらかのハトがいるとします。以下、同様の記法を採用します。あなたがボスハトを右下に動かす手は当然合法ですが、実際に実行すると

	x
x	B	x
	x

となり、あなたの負けとなります。このように、実行すると即座にあなたのボスハトが囲まれてしまう手が存在します。もし仮に、ある手番のときに、このような自滅する手しかないとしたら、相手の手番に回る前に敗北することが確定してしまいます。
この記事の目標は、千日手禁止ルールが無い条件の下で、実は自滅しない手が必ずあることを示すことです。これが示されれば、勝敗が確定するのは、必ずいずれかのプレイヤーが自分が勝つ手を選択したときである、ということが分かります。解析がスッキリして便利ですね。

考えるべき状況の整理

大筋で行うことは反例探しの旅です。「この盤面だとどの合法な手でも自滅する手しかない」といった盤面を探し、まったく見つからないことが分かれば主張の証明完了です。
まず自分に手番が回ってきたということは、自分のボスハトの四方がハトで囲まれている状況ではない、ということになります。もし仮に四方のうち空いているマスに自分のボスハトを動かす手が合法なら、元いた位置がちょうどボスハトの四方の空きマスの役割を果たすので、これは自滅しない手です。
言葉では分かりにくいので図にします。例えば以下の状況のときを考えます。

	x	x
x	B
	x	x

ボスハトの右側が空欄になっていて、さらにボスハトを右側に動かす手は合法です。実際に右側に動かすと

	x	x
x		B
	x	x

このような盤面になります。このときボスハトの左側は必ず空欄になるはずです。なぜなら、そこはまさに先ほどまでボスハトがいた場所で、移動したことによって空欄になっているからです。よってこれは自滅しない手です。
したがって考えるべき状況は、自分のボスハトを四方のいずれに動かす手も合法でない場合のみとなります。
空欄があるのに動かすのが合法でない場合というのはどういう状況でしょうか？ハトを動かす際は、ルール上4つの判定がなされます。

• その移動はそのハトの種類から決まる移動条件に合致するか
• 移動先または移動経路に障害となるハトはいないか*2
• 移動した結果、盤面のサイズは4x4のスペースに収まるか
• 移動した結果、いずれかのハトが孤立*3しないか

これらの条件をすべてクリアしたら、その移動が合法な手となります。
改めて今回のボスハトを動かす場合について考えましょう。1つ目と2つ目の条件は明らかにクリアします。3つ目は「壁が元々ある場合はその方向は空欄とはみなさない」とすることで*4、ハトの移動によって盤面のサイズが広がることはないことが分かるので、やはり条件を満たすことが分かります。よって肝になるのは4つ目の条件となります。つまり自分のボスハトを四方のいずれの空欄に動かそうとしても、孤立するハトが出るという状況を考えればよいです。
さらに踏み込んで、ボスハトを動かすことで孤立するハトが生まれるのはどういうときか考えます。当たり前ですが、ボスハトを動かした場合でも、他のハトは一切移動しません。つまりボスハト以外との間の隣接関係は全く変化しません。ということは、ボスハトが移動したことによってあるハトが孤立するためには

• 移動前にはボスハトと辺または角で接していた
• 移動後にボスハトと辺でも角でも接しなくなった上、ほかのハトとも辺でも角でも接していなかった

が重なる必要があります。1つ目の条件から、孤立候補のハトは移動前のボスハトの位置の八方の隣接マスにしかいないことが分かり、2つ目の条件から「ボスハトを仮に取り除くと孤立する」という条件を満たす必要があります。
以上を踏まえて、具体的にいくつかのパターンに分けて考えていきます。

ボスハトが4x4の隅にいるとき

元からボスハトが孤立している状況では手番が回ってこないため、ボスハトの周辺にはすくなくとも1羽のハトがいます。またボスハトの周辺にハトが2羽以上いる場合、それら同士で辺または角で接しているため、ボスハトを取り除いても孤立しません。したがって考えるべき状況は
(1)

x	x
B	x

および
(2)

	x
B

の2通りです。いずれもボスハトを右に動かす手が合法です。

ボスハトが4x4の隅にはいないが縁に接しているとき

ボスハト周辺で孤立しうるハトがあるような場合のみ列挙すると、以下の6通りになります。
(1)

		x
x	B	x

(2)

x
x	B	x

(3)

		x
x	B

(4)

x		x
	B

(5)

x		x
	B	x

(6)

x	x	x
x	B	x

それぞれ例えば(1)~(5)は上方向への移動が、(6)は右方向への移動が合法となります。

ボスハトが隅にも縁にもいないとき

これまでと同じ考え方で、9通りのパターンが考えられます*5。これまでと同様、それぞれについてすぐに合法と分かる動きを考えるのですが、実は合法な動きが必ずしも特定されないものが以下の3パターンあります。
(1)

x
	B
		x

(2)

x		x
	B
		x

(3)

x		x
	B
x		x

いずれの場合についても「対角に位置するハトのペアであって、ボスハトを取り除くと同時に孤立するものが存在する」が満たされることが、合法な移動がないための必要十分条件となります。もし「~~が存在しない」なら、孤立しうるものたちがいる方向にボスハトを移動すれば合法ですし、「~~が存在する」なら、どう動かしても孤立するハトが生まれてしまって合法でなくなります。
ここから先は具体的にハトを並べる必要があります。ですが、ひとつだけ探索の手がかりとなる条件を出すことができます。
もし仮に手持ちのハトがいるとします。すると(1),(2),(3)のどのパターンでも、ボスハトの周辺のいずれかには配置できます。元の目的は「自滅しない手がある」ことを示すことだったので、この場合は考えなくてよいことが分かります。すなわち、「すべての手が自滅する手である」という状況があるとしたら、その時点であなたのハトはすべて盤面上になくてはなりません。さらに、ルール上相手のボスハトも当然盤面上に存在する必要があるため、都合7羽のハトが少なくとも盤面上にいる場合を考えればよいことになります。
この手がかりを元に、各パターンについてより具体的に並べてみます。

パターン(1)

ボスハトの周辺の2羽はどちらも「ボスハトを取り除くと孤立する」ようにする必要があります。そのようなパターンは以下の2通りのみとなります。
(1-a)

		y	y
x			y
	B
		x

(1-b)

y
		x
	B
x			y

ここで y はハトがいる、または空欄とします。以下でも同様の記法を採用します。いずれでも盤面上に7羽のハトが存在しえないので、いずれも考える必要のないパターンです。(すなわち手札からボスハトの横に出す手が合法)

パターン(2)

対角に位置するハトを「ボスハトを取り除くと孤立する」ような状態にするパターンは以下の3通りです。
(2-a)

y
		x
	B
x		x	y

(2-b)

		y	y
x			y
	B
x		x

(2-c)

		y	y
x		x	y
	B
		x

(2-a)は7枚のボスハトが存在できないので不適です。(2-b),(2-c)はギリギリ7羽のハトが存在できます。ただ x, y たちのうちいずれかの自分のハトは動かせるため、これが自滅しない手となります。具体的には、アニキハト、ヤイバト、トツハトあたりを上下左右のいずれかに1マス動かす操作を考えればよいでしょう。

パターン(3)

右上と左下を孤立候補とするパターンと、左上と右下を孤立候補とするパターンの2通りが考えられます。
(3-a)

y
x		x
	B
x		x	y

(3-b)

		y	y
x		x	y
	B
x		x

(3-a)は最大7羽です。xのいずれかにはアニキハト、ヤイバト、トツハトのいずれかが居るので、上下左右のいずれかの方向の合法な動かし方があります。
(3-b)は最大8羽です。yはすべてハトか、1つだけ空欄です。もしyのひとつが空欄なら、やはりxのいずれかにアニキハト、ヤイバト、トツハトのいずれかが居るので、上下左右のいずれかの方向の合法な動かし方があります。yがすべてハトの場合、yに上記3ハトが集まっていない場合は同様の論法で合法な自滅しない手があることが分かりますし、集まっている場合でも隅でないyを動かす手が合法な自滅しない手となります。
これですべての場合を調べ尽くしました。どの場合でも、自滅しない合法な手が必ずありました！

まとめ

以下をポイントに自滅しない手を探索しました:

• 基本的にボスハトが上下左右に移動する手があること
• ボスハトの周りに孤立ハト予備軍がいる場合のみ要注意なこと
• その場合でも手札から出したり適当な別のハトを動かすことで自滅しないこと

その結果、常に自滅しない手があることが分かりました。晴れてスッキリ探索ができて私は嬉しいです。

次回は局面数の見積もりみたいな話をしたいです。

*1:前回の記事を参照

*2:ハジケハトの場合は移動経路判定なし

*3:ハトが孤立するとは「そのハトの八方のいずれにもハトがいないとき」と定めます。

*4:実際、自分の手番が回ってくるということは、壁以外の方向に空欄があることも保証しています。

*5:列挙するのが面倒くさいので全列挙は読者の演習問題とします。

【Tokyo Doves】ダイソーで買ったハトのボドゲが面白かったのでルールを考察してみた

先日ダイソーで「トウキョウのハト エサバ・バトル」(英語名 Tokyo Doves) というボドゲを買いました（こんなゲームです↓）。もちろん100円です*1。

couple-game.net

なんか以前ネット上でバズったゲームらしく、100円で買えるのが驚きなほど面白くて奥深いゲームです。あまりにも面白いので、ここ最近ずっとこのボドゲの解析をして遊んでいます。
その中で「ちょっと元々のルールだと足りないんじゃないか？」と感じる部分があったので、メモがてら記事にしたいと思います。具体的な解析してみた話はまた別記事で。

通常ルール

冒頭の記事を読んでください（サボり）
実際遊んでみると分かるのですが、幅が4になったときに壁ができること、また4でなくなると壁が消え去るというのがなかなかに曲者で、このゲームの醍醐味となっています。終盤に差し掛かって「よし詰ませたかな？」と思っても、壁が現れたり消えたりすることで思いもよらない逃げ道が残っていたりします。また終盤は必然的に両プレイヤーのハトがひしめき合う形になるのですが、相手のハトを詰ませているつもりが自分のハトが詰んでいた・・・みたいなこともまま起こるため、気の抜けない戦いとなります。

ちなみに冒頭の記事には無いものの「ハトを出す」「ハトを移動する」の他に「ハトを戻す」という操作もオプションルールとして用意されています。以下がルールブックでの記述です:

●ハトを戻す
場にある自分の好きなハトを１つ選び、手札に戻すことができます。
・戻したらすぐに手番が終了します。
・戻した後に、他のハトと辺とも角とも接していないハトが出てしまうようにすることはできません。
※このルールは慣れてから追加しましょう。慣れてからも入れるかどうかは相手と相談してください。

この選択肢がなくても遊べはするものの、このルールがある方がグッとゲームの深みが増すので、以下では採用することにします。

通常ルール深堀り

ゲームの対称性

6種類のハトはいずれも上下左右の反転及び90°の回転に対して対称です。ボードやルールにも向きが存在していません。強いていえば初期配置のみ向きがありますが、仮に初期配置を上下左右の反転や90°回転させたところでゲーム進行は全く変わりません。

ゲームの終了条件

自分のボスハトの四方を別のハトまたは壁に囲まれると、即座に敗北が確定します。その他ルールブックには「※パスという甘い選択肢はありません、即負けです。」とあります。つまり、自分の手番でどの操作も不可能であることが分かった場合は負けになります。実はハトを戻すという操作をありにすると、通常ルールの範囲で「手番中どの操作も行うことができない」というケースはなくなります*2。ちなみに（おそらく起こる頻度は低そうですが）両者のボスハトが同時に囲まれた場合の取り扱いは規定がありません。ルールブックの文言を文字通り受け取れば「両者敗北」ですが、これを引き分けとするか、動かした側が勝ちとするか負けとするかは、解釈次第かと思います。個人的には勝ちか負けかどちらかを採用したほうが明確でよいかなと思います。また千日手（同じ盤面を何度も繰り返してしまう状態）に対する規定が全くありませんが、終盤はかなり千日手間際の場面が登場しがちです。この点は提案したいルールがあるので後述します。

先手必勝？後手必勝？or else？

ゲームの分類のひとつに「二人零和有限確定完全情報ゲーム」というものがあります↓
ja.wikipedia.org
詳しい説明は上を読んでいただくとして、これに分類されるゲームは最善手を指し続けた場合に先手必勝・後手必勝・引き分けのいずれかが定まるようなものになっています。Tokyo Doves は千日手の存在さえなんとかできれば、この分類に属することができます。やはり千日手のルールぎめがポイントです。

ちなみに、通常ルールの範囲だと後手必勝でないことは次のようにすぐに示せてしまいます:
もし仮に後手必勝だとすると、先手がどのように指し続けたとしても、後手が適切に対応することでかならず勝利することができます。先手が一番最初に自分のボスハトを斜めに動かしたとします。その結果の盤面は初期の盤面を90°だけ回転したものになっていますが、これは初期の盤面とルール上意味が変わりません。すなわち事実上後手の立場を獲得したわけです。したがって後手必勝の仮定を再び用いて、後手がどのように指し続けたとしても、先手が適切に対応することでかならず勝利することができます。これらを同時に成立させるような状況はないので、後手必勝ではないことが示されたことになります。

ルールの提案

千日手対策ルール

結論からいうと、以下のルールを追加することを提案したいです。

●千日手禁止ルール
「ハトを出す」「ハトを動かす」「ハトを戻す」のいずれの操作によっても、その結果実現される盤面が、それまでの相手の手番の操作前に実現した盤面と一致してはならない。

柔らかい言葉でいえば、何らかの操作を実行して相手の手番になった時点で「え？これ何回か前の自分の手番のときと同じ盤面だよ？」となってはいけない、ということです。そうなってしまうような操作を禁止することで、二度と同じ盤面が実現しない＝千日手が起こらないという形になります。ゲームの対称性を鑑みれば、より強い以下の制約でもよいかもしれません。コンピューター的にはこのほうが自由度が絞れるので都合が良かったりします。

●千日手禁止ルール（強）
「ハトを出す」「ハトを動かす」「ハトを戻す」のいずれの操作によっても、その結果実現される盤面が、それまでの相手の手番の操作前に実現した盤面およびそれを反転または回転したものと一致してはならない。

ただ人間同士で遊ぶ場合であれば、反転・回転で一致するかどうかの判定はなかなか厳しいかもしれません。また「見落としていてうっかり」というケースありそうです。実際は以下のようなゆるいルールのほうが運用上は便利かもしれません。

●千日手禁止ルール（弱）
相手の手番の操作によって実現した盤面が、過去の自分の手番の開始時に実現したことのある盤面に一致していた場合、その旨を指摘することでその操作を取り消し、相手の手番をやり直させることができる。相手はその手番で全く同じ操作を実行することはできない。なお盤面が一致した時点での自分の手番の操作を実行した後に指摘した場合は無効となる。

先手の優位性に対する制限

先手が斜めに動かすと事実上の後手に回ることができるということはすでに述べました。千日手禁止のルールを採用することで事実上の後手ではなくなるのですが、さらに踏み込んで以下のルールを採用するのはいかがでしょうか。

●初期盤面に関する制約
先手・後手共に、自分の手番の操作の結果、初期盤面およびそれを反転または回転したものと一致する盤面を実現してはならない。

単にそれぞれのボスハトが辺で接していて他のハトがいない、という状態を本当の初期のみに制限するというルールです。これで先手と後手の自明な対応は崩れるので、よりルールが面白くなるのではないでしょうか。

同時囲みルール

すでに述べましたが、一応明文化しておきます。ひとつの方法を採用しておきます。

●同時にボスハトが囲まれた場合の取り扱い
プレイヤーAの操作によって両プレイヤーのハトの四方が同時に別のハトまたは壁に囲まれた場合、プレイヤーAの敗北とする。

ルール採用の影響

上記で提案したルールを採用した場合、いくつか状況が変わるものがあります。ポイントを箇条書きにしてみます。

• 千日手がなくなるので晴れて先手必勝・後手必勝の議論ができる。
• 自分の手番で実行可能な操作がない、という状況が理論上起こりうる。ルールブックに則り、その場合はそのプレイヤーの敗北。
• 引き分けがないので、かならず先手か後手が必勝である。

次回以降（あれば・・・）の解析の紹介では、これらのルールの下で説明したいと思います。

*1:クソリプがあったので補足ですが、税込みだと110円です。

*2:ボスハト以外が盤面にあるならそれを戻す操作が可能ですし、もしいなくてボスハトが動けないとしたら、その時点ですでに勝敗が確定しているはずです。

Rust の文字列操作がややこしいので Python の記法と比べながらまとめてみた

重要：この記事の微妙な点に補足を入れたバージョンを再投稿しました↓
smooth-pudding.hatenablog.com

最近 Rust にハマりつつあるぷりんです。n 番煎じですが、Rust の文字列操作をまとめてみました。せっかくなので、個人的に一番親しみのある Python の構文と比較しながら見ていきます。

参考にしたサイト

やはりいろんな方が苦労されているようで、いろいろなところで記事があります。特に参考にした頻度の高いものを挙げておきます。

text.baldanders.info
↑個人的に一番まとまっているように感じました。最後の切り出しの苦労はなんか共感してしまいます。

doc.rust-jp.rs
↑公式です。いくつかの書き方は紹介されているものの、網羅的とは言えないような印象です。

note.com
↑ユーザー視点でのつまづきポイントも拾いながら紹介されています。

qiita.com
qiita.com
↑いずれも文字・文字列型の間の変換がまとまっています。

他にもたくさん記事があるので調べてみてください。

文字/文字列の定義

Python では str 型のみがあり、シングルクォーテーションマークまたはダブルクォーテーションマークで挟んで定義できます。Python に文字型はありません(たぶん)。

# Python
s = "Hello"
t = 'World' # "World" と等価
u = 'c' # "c" と等価

一方 Rust では文字列を表す String 型, &str 型と文字を表す char 型があります。単純にダブルクォーテーションマークで挟んだものは &str 型となり、String 型を作るには適切に変換する必要があります。

// Rust
fn main() {
    let s = "Hello"; // &str 型
    let t1 = "World".to_string(); // String 型
    let t2 = String::from("Nice"); // String 型
    let t3 = "Good".to_owned(); // String 型
    let t4: String = "Happy".into(); // String 型
}

イメージとしては &str は長さが決まっていて「固い」文字列、String は長さが可変の「柔らかい」文字列という感じです(もちろん変更を加えるには mutable にする必要はあります)。文字列の編集については後ほど紹介します。
一方 char 型はシングルクォーテーションマークで挟んで定義します。複数の文字を含めることはできません。

// Rust
fn main() {
    let c = 'c'; // char 型
}

それぞれの型の間の変換

Python はそもそも全部同じ str 型なので当然変換自体がありません。
Rust はいろいろな変換方法があります。冒頭でも紹介した以下のサイトが詳しいです。
qiita.com
qiita.com
上記のサイトを含めて String → &str は & をつければいい、としか紹介されていないところが多いので、他の方法もいくつか紹介しておきます。

// Rust
fn main() {
    let s = "abc".to_string();
    let t1 = &s; // よく紹介されている方法
    let t2 = s.as_str(); // .as_str() で変換
    let t3 = &s[..]; // 全体のスライスの参照
    let t4 = &*s; // deref の ref (まだ理解できません...)
}

&String と &str は別物な気がするのですが、なぜ & を付けるだけで &str になるかはよくわかりません。。。
また char 型から &str に変換する方法は一旦 .to_string() で String を経由してから &str にする方法がよく紹介されています。ただ String に変換するときに動的メモリ確保が動いてオーバーヘッドが発生するらしいので、気になる場合は以下の記事のコメント欄にある方法を利用するとよさげです。
qiita.com

// Rust
fn main() {
    let c = 'a'; // char 型
    let mut buffer = [0u8; 4];
    let s: &mut str = c.encode_utf8(&mut buffer); // "a"
}

文字列の結合

Python では足し算記号のほか、format を使ってつなげることができます。

# Python
s = "abc"
t = "def"
u1 = s + t
u2 = "%s%s" % (s, t)
u3 = "{}{}".format(s, t)
u4 = f"{s}{t}" # 個人的に一番好き

一方 Rust でも足し算記号で結合できますが、左辺は String 右辺は &str である必要があります。結合後は String になります。

// Rust
fn main() {
    let s = "abc".to_string(); // String 型
    let t = "def"; // &str 型
    let u = s + t; // String 型
}

なおこのタイミングで s の値の所有権は u に移るため、このあと s は参照できなくなります。これを避けるためには他の手法を使うか、.clone() を挟めばOKです。

// Rust
fn main() {
    let s = "abc".to_string(); // String 型
    let t = "def"; // &str 型
    let u = s.clone() + t; // String 型
    println!("{}", s); // 参照可能
}

Rust でも format を利用することができ、format! マクロで実現できます。これは String, &str, char のいずれからも実行できます。結合後は String になります。また所有権の移動もありません。

// Rust
fn main() {
    let s = "abc".to_string(); // String 型
    let t = "def"; // &str 型
    let c = 'g'; // char 型
    let u1 = format!("{}{}", s, t); // "abcdef" の String 型
    let u2 = format!("{}{}", s, c); // "abcg" の String 型
    let u3 = format!("{}{}", t, c); // "defg" の String 型
    let u4 = format!("{}{}{}", s, t, c); // "abcdefg" の String 型
}

Rust の String は Vec に似ていて、push (char を繋げる用) や push_str (&str を繋げる用) を使って後ろに延長することが可能です。当然もとの String は mutable である必要があります。

// Rust
fn main() {
    let mut s = "abc".to_string(); // mutable な String 型
    let t = "def"; // &str 型
    let c = 'g'; // char 型
    s.push_str(t); // "abcdef" の String になる
    s.push(c); // "abcdefg" の String になる
}

なお (見た目に反して?) t や c の所有権は移動せず、この後も参照できます。
他にも一旦 char のイテレーターにしてから結合するという技もあるようです。.chars() は String, &str のいずれでも使えて、構成要素となる文字 (char 型) が順番に出てくるイテレーターを生成します。イテレーター同士は .chain() で結合できて、そのあと .collect() で String にまとめています。なお所有権は移動しません(なんで？？？)。

// Rust
fn main() {
    let s = "abc".to_string(); // String 型 (&str 型でもOK)
    let t = "def"; // &str 型 (String 型でもOK)
    let u: String = s.chars().chain(t.chars()).collect(); // 左辺で型を書く必要あり   
}

collect は「左辺で指定した型に応じて値を集めてまとめる」というメソッドなので、型指定は必須です。あるいは collect の型テンプレートを手で指定することも可能です(が、今回は左辺で型指定するほうがスマートでしょう)。

// Rust
fn main() {
    let s = "abc".to_string(); // String 型 (&str 型でもOK)
    let t = "def"; // &str 型 (String 型でもOK)
    let u = s.chars().chain(t.chars()).collect::<String>();
}

ちなみに Python でも itertools.chain を使えば同じやり方が可能です。Python では文字列そのものが文字のイテレーターになるので*1、それらをくっつけたイテレーターを作って join でつなげます。

# Python
from itertools import chain

s = "abc"
t = "def"
u = "".join(chain(s, t))

文字列の繰り返し

Python では掛け算記号で実現できます。

# Python
s = "a" * 5 # "aaaaa"

一方 Rust では掛け算記号は使えませんが、.repeat() というメソッドがあります。繰り返す元は String か &str が使えて、結果は String になります。所有権は移動しません。

// Rust
fn main() {
    let s = "a".repeat(5); // "aaaaa" という String
    let t = "a".to_string(); // String 型
    let u = t.repeat(5); // "aaaaa" という String
}

char を繰り返したい場合は一旦 String または &str に変換してから上記の方法を使うか、何らかの方法で同じ要素を持った配列なり Vec なりを作った後に .iter() でイテレーターにして .collect() するとよいかもしれません。

// Rust
fn main() {
    let c = 'a'; // char 型
    let s: String = [c; 5].iter().collect(); // "aaaaa" という String
}

なお変数の値で繰り返し回数を決めたい場合は上記の書き方ではうまくいかないので、諦めてさっさと String なり &str なりに変換してしまうほうが手短だと思います。

文字列の切り出し

追記: 以下の方法は全角文字などが現れる場合はうまくいかないようです。以下の記事を参照してください。
qiita.com

Python では文字の入った配列のごとく扱うことができます。

# Python
s = "abcdefg"
t1 = s[0] # "a"
t2 = s[-2] # "f"
t3 = s[:3] # "abc"
t4 = s[1:] # "bcdefg"
t5 = s[2:-1] # "cdef"

Rust でもほぼ同様の書き方ができますが、切り出した後に & を付ける必要がある点が要注意です。結果は &str 型です。

// Rust
fn main() {
    let s = "abcdefg"; // String 型でもOK
    let t1 = &s[0..=0]; // "a" (Python でいう s[0:1])
    let t2 = &s[s.len()-2..=s.len()-2]; // "f" (Python でいう s[-2:-1])
    let t3 = &s[..3]; // "abc"
    let t4 = &s[1..]; // "bcdefg"
    let t5 = &s[2..s.len()-1]; // "cdef"
}

範囲指定の上限は Python だと外側にあっても OK でしたが、Rust だと (正しく？) panic するみたいなので要注意です。
特定のインデックスの位置にある char を取り出したい場合は .char() で文字のイテレーターを作ったあと .nth() で取り出せばOKです。インデックスの外側を参照しても即座には panic しないように、返ってくる値は Option<char> (つまり Some(文字) か None)になっています。Some の中身を取り出すには .unwrap() を使います。

// Rust
fn main() {
    let s = "abcdefg"; // String 型でもOK
    let t1 = s.chars().nth(0).unwrap(); // 'a'
    let t2 = s.chars().nth(s.len()-2).unwrap(); // 'f'
}

インデックスの外側を参照する恐れのある場所であれば、単に .unwrap() するのではなく .unwrap_or_else() したり、もっと真面目にパターンマッチしたりしてエラーハンドリングするようにしましょう。(Python でいうと try ~ except IndexError で挟むのに対応します)
Python では増大幅を指定して歯抜けに取り出すのも簡単です。特に増大幅を負の数に設定することで逆順も可能です。

# Python
s = "abcdefg"
t1 = s[::2]  # "aceg"
t2 = s[2::3] # "cf"
t3 = s[::-1] # "gfedcba"

Rust では、イテレータの操作を頑張ればなんとか実現できます。

// Rust
fn main() {
    let s = "abcdefg"; // String 型でも可
    // ↓"aceg" という String
    let t1: String = s.chars().step_by(2).collect();
    // ↓"cf" という String
    let t2: String = s[2..].chars().step_by(3).collect();
    // ↓"gfedcba" という String
    let t3: String = s.chars().rev().collect();
}

その他細々とした文字列操作

その他文字列操作でよく使う気がする Python 関数たちを列挙しておきます。

# Python
"aa,b,ccc".split(",") # ["aa", "b", "ccc"]
" abc  ".strip() # "abc"
"abcde".replace("a", "A") # "Abcde"
"abCdE".to_upper() # "ABCDE"
"abCdE".to_lower() # "abcde"
"hello".starts_with("he") # True
"hello".ends_with("llo") # True
"ll" in "hello" # True

Rust だとこんな感じです。

// Rust
fn main() {
    let s = "aa,b,ccc"; // String でも可
    let v: Vec<_> = s.split(",").collect(); // ["aa", "b", "ccc"]: Vec<&str>
    let s = " abc  "; // String でも可
    let t = s.trim(); // "abc": &str 型
    let s = "abcde"; // String でも可
    let t = s.replace("a", "A"); // "Abcde": String 型
    let s = "abCdE"; // String でも可
    let t = s.to_uppercase(); // "ABCDE": String 型
    let t = s.to_lowercase(); // "abcde": String 型
    let s = "hello"; // String でも可
    let b = s.starts_with("he"); // true
    let b = s.ends_with("llo"); // true
    let b = s.contains("ll"); // true
}

最後に

まだ勉強仕立てで不十分な内容もあると思いますので、ご指摘歓迎です。

*1:厳密には for 文などが呼ばれるタイミングなどで some_object.iter() というメソッドが呼ばれてイテレーターが返ってきますが、some_object が str 型の場合は構成要素の文字が順々に出てくるイテレータが返ってきます。

改良版じゃんけん「ツーペン」の効率について

こんにちは。最近「ゆる言語学ラジオ」という youtube チャンネルをよく視聴するのですが、そのチャンネルのとある動画でじゃんけんの改良版「ツーペン」が紹介されていました↓

動画ではルールの紹介のあと、通常のじゃんけんとの効率性の比較の際に数学が役に立ったというエピソードが続きます。そこでこの記事ではこの検証を改めてやってみたいと思います。

ルール

ツーペンでは、以下のルールに則って2人以上の参加者から1人の勝者を決めることができます。

• 以下を基本手順と呼ぶこととする:

開始時の参加人数を とする。
【 の場合】

1. 2人をそれぞれ親または子とする
2. 「ツーペン！」の掛け声とともにそれぞれグーまたはチョキを出す
3. 手が同じなら親の勝ち、手が異なるなら子の勝ち

【 の場合】

1. 「ツーペン！」の掛け声とともにそれぞれグーまたはチョキを出す
2. それぞれの手を出した人数を数える
3. 小数の手を出した人が勝ち。ただし全員同じ手の場合やちょうど半々の場合は全員あいことする。

• 基本手順を実行して勝者(またはあいこ)のみを残すことを繰り返すことで参加者を減らしていき、最終的に残った1人を全体の勝者とする。

比較のため、通常のじゃんけんのルールも同様の形式で書いておきます。

• 以下を基本手順と呼ぶこととする:

1. 「じゃんけんぽん！」の掛け声とともにグーまたはチョキまたはパーを出す
2. 全員の手が2種類のみに分かれた場合に、強い手を出した人が勝ち。1種類または3種類の場合は全員あいことする。

• 基本手順を実行して勝者(またはあいこ)のみを残すことを繰り返すことで参加者を減らしていき、最終的に残った1人を全体の勝者とする。

ポイントの整理

効率性の観点でのじゃんけんと比較したときのツーペンの利点は

• あいこがない
• 少数派が残るためかならず 1/2 以下になる

ことです。通常のじゃんけんは大人数になると勝敗がなかなか決まらない上、決まってもあまり人数が減らない可能性があるため、それらを改良した形となります。
一方でツーペンと比べた場合のじゃんけんの利点は

• あいこ判定に必ずしも全員の手を調べる必要がない

ことです。あいこがすぐ判定できるというのはそれなりに時間の節約に役立つものの、ツーペンではそもそもあいこになる確率が低いため、おそらく総じてツーペンのほうが有利になるでしょう。
上記の点を踏まえて、1人の手を確認するのにかかる時間を「1ステップ」という単位で数えて、最後の1人が絞り込まれるまでに平均で何ステップ必要かで比較したいと思います。

勝敗決定までにかかる時間の検証

状態遷移の考え方を導入します。参加人数 の状態から、一回の基本手順で参加人数 の状態に移ることを という風に書くこととします。あいこの場合は の場合に相当します。この記法により、あいこの場合と勝敗が決まった場合を同じように取り扱うことができます。さらに参加者数が のときに基本手順の結果状態遷移 を起こす確率を 、またその際の平均的に必要なステップ数を と表すこととします。さらに複数回の基本手順を含めて最終的に1人の勝者を決めるまでに必要な平均的なステップ数を とします。このとき

が成立します。両辺に が入っているので、整理して について解いてみると

が得られます。よって、 と と が分かっていれば を求めることができます。 については帰納的に定めることができるので、残りの および をどうやって求めるか考えてみましょう。

普通のじゃんけんの場合

まず について考えます。 の場合は 人が勝つパターンなので、勝つ人を選ぶ 通り、勝ち負けの2種類の手の選び方 通りで、都合 通りあります。よって となります。 の場合、すなわちあいこのときは、手の種類が2種類でない場合に相当するので、全部で 通りあります。よって となります。以下にまとめておきます:

次に について考えます。 の場合は、 人のうちひとりだけ手を変えるとあいこになりうることを考えれば、 であることが分かります。一方で についてはある3人が別々の手を出していることを発見すればその時点であいこになってしまいます。よって、一人ひとりの手を順番に見ていったときに、 人目の手を確認したときにはじめて3種類の手が揃う確率、などを考慮する必要があります。すべて説明すると時間がかかりまくるので途中省略すると、

となります。人数が多いときはおおよそ5.5人ぐらい確認するとあいこが判明するようです。6人以上でじゃんけんするときは結構辛くなりそうな予感がします。

ツーペンの場合

まず について考えます。 のときは勝敗が必ず決まるので です。以下 とします。 の場合、 のときは です。なぜなら勝つのは決まって少数派だからです。 の場合は、勝つ人の選び方が 通り、少数派が選ぶ手の種類が 通りなので、合わせて 通りあります。よって となります。 の場合、すなわちあいこの場合は が奇数の場合は , が偶数の場合は として となります。以下にまとめておきます:

次に について考えます。実は によらず が成立します。これは全員の手が判明するまで基本手順の結果が(あいこの場合も含めて)決まらないことから分かります。すなわち仮に 人の手が決まったとしても、最後のひとりが残るのか脱落するのか判定できません(どちらの手を出すかによって結果が変わる)*1。よって必ず ステップ必要で、 ステップあれば OK となります。

数値計算の結果

を手計算するのは現実的ではないので、python で書き飛ばしコードを作ってプロットしてみました。

その差は歴然です。通常のじゃんけんの方は人数に対して指数関数的に伸びているのに対し、ツーペンでは概ね線形で抑えられています。例えば の場合は5倍近くの差があるようです。

効率性以外のツーペンの問題点

• 人数が多いときにどちらが勝ちか判定しづらい

ふつうのじゃんけんなら「グーが勝ち」とわかりやすいですが、ツーペンだと数えないと勝敗が決まらないのでふわっとするかもしれません

• 1回の基本手順にかかる時間が長い

頑張って数えないといけないのでやや間延びするかもしれません。今回の検証では手の確認を普通のじゃんけんとツーペンで同じとみなしましたが、現実的には「種類を数える」のと「個数を数える」のではしんどさが違いそうです。それも含めて評価するとよいかもしれません。

• ルール説明の時間がかかる

これはデファクトスタンダードの力ですね。意外とここがネックになりそうな気がします。例えば代表者とじゃんけんする方式とどちらが現実的に有効か、というのも検証すると面白そうです。

*1: "でない" ことは早めに分かるかもしれませんが、基本手順がすべて終わるためには全員の勝敗またはあいこが定まる必要があり、そのためには全員分の手を確認する必要があります。

デコレータで遊ぶ(python) :: 特定の時間以外は挙動を変える

こんにちは。
ふとデコレータで遊びたくなったので書いてみました。

import datetime as dt
from typing import Callable


def time_limit(begin: dt.time, end: dt.time, default: Callable):
    def deco(func: Callable):
        def wrapper(*args, **kwargs):
            now = dt.datetime.now().time()
            if (begin <= now <= end) \
                    or (now <= end < begin) \
                    or (end < begin <= now):
                return func(*args, **kwargs)
            else:
                return default(*args, **kwargs)

        return wrapper

    return deco


def off_mode(*args, **kwargs) -> str:
    print("No, I'm off mode now.")
    return "Do nothing"


@time_limit(dt.time(9), dt.time(17), off_mode)
def pass_task(task: str) -> str:
    print(f"Sure, I'll do that task '{task}'.")
    return "I'm doing it"


if __name__ == '__main__':
    response = pass_task("wash dishes")
    # Case1: No, I'm off mode now.
    # Case2: Sure, I'll do that task 'wash dishes.'
    print(response)
    # Case1: Do nothing
    # Case2: I'm doing it

おまけで、一定の時間内に終わらなければ関数の実行を強制終了するデコレータも作ってみました

import time
import threading
from queue import Queue


def stop_in_10_sec(func):
    q_master = Queue()
    q_return = Queue()

    def stopper():
        time.sleep(10)
        q_master.put("")

    def func_with_queue(*args, **kwargs):
        nonlocal q_return, q_master
        q_return.put(func(*args, **kwargs))
        q_master.put("")

    def wrapper(*args, **kwargs):
        th_master = threading.Thread(target=q_master.get)
        th_func = threading.Thread(target=func_with_queue, args=args, kwargs=kwargs)
        th_func.setDaemon(True)
        th_stopper = threading.Thread(target=stopper)
        th_stopper.setDaemon(True)

        th_master.start()
        th_func.start()
        th_stopper.start()
        th_master.join()
        if q_return.empty():
            raise TimeoutError
        else:
            return q_return.get_nowait()

    return wrapper


@stop_in_10_sec
def count_up():
    for i in range(20):
        print(i)
        time.sleep(1)
    return "Finished!"


if __name__ == '__main__':
    print(count_up())  # 9 まで数えて停止

よっしゃできた〜と思ったあたりで、実は timeout_decorator というパッケージがあることを知りました。車輪の再発明だった〜〜〜

import timeout_decorator


@timeout_decorator.timeout(10)
def count_up():
    for i in range(20):
        print(i)
        time.sleep(1)
    return "Finished!"


if __name__ == '__main__':
    print(count_up())  # 9 まで数えて停止

追記(2021/10/21):: さらにおまけで、指定した時間外になると、実行中でも中止されるようなデコレータを作りました。もしかしてこれも車輪の再発明・・・？(震声)

import datetime as dt
from functools import wraps
from threading import Thread
import time
from typing import Callable, Any
from queue import Queue


class TimeInterval:
    def __init__(self, begin: dt.time = dt.time.min, end: dt.time = dt.time.max):
        self.__begin = begin
        self.__end = end

    @property
    def begin(self) -> dt.time:
        return self.__begin

    @property
    def end(self) -> dt.time:
        return self.__end

    def __str__(self) -> str:
        return f"{self.begin:%H:%M:%S.%f} - {self.end:%H:%M:%S.%f}"

    def __contains__(self, item) -> bool:
        if isinstance(item, dt.time):
            return (self.begin <= item <= self.end) \
                   or (item <= self.end < self.begin) \
                   or (self.end < self.begin <= item)
        raise NotImplemented


class OvertimeError(Exception):
    pass


class WorkTimeManager:
    def __init__(self, begin: dt.time = dt.time.min, end: dt.time = dt.time.max):
        self.__work_time = TimeInterval(begin, end)
        self.__now = dt.datetime.now().time()
        self.__q_master = Queue()
        self.__q_return = Queue()

    # ----- for time control -----
    def update_now(self) -> None:
        self.__now = dt.datetime.now().time()

    def is_overtime(self) -> bool:
        return self.__now not in self.__work_time

    def raise_overtime_error(self) -> None:
        err_msg = f"It's {self.__now}, " \
                  f"out of work time ({self.__work_time})"
        raise OvertimeError(err_msg)

    # ----- for queue control -----
    def notify_master(self) -> None:
        self.__q_master.put("")

    def await_notification(self) -> None:
        self.__q_master.get()

    def put_return_value(self, value) -> None:
        self.__q_return.put(value)

    @property
    def yet_returned(self) -> bool:
        return self.__q_return.empty()

    def get_return_value(self) -> Any:
        return self.__q_return.get_nowait()


def work_time(
        begin: dt.time = dt.time.min,
        end: dt.time = dt.time.max,
        check_frequency: float = 1.,
):
    def deco(func: Callable) -> Callable:
        man = WorkTimeManager(begin, end)

        def func_for_q(*args, **kwargs) -> None:
            man.put_return_value(func(*args, **kwargs))
            man.notify_master()

        def keep_time(freq: float) -> None:
            while True:
                man.update_now()
                if man.is_overtime():
                    man.notify_master()
                    break
                time.sleep(freq)

        @wraps(func)
        def wrapper(*args, **kwargs) -> Any:
            if man.is_overtime():
                man.raise_overtime_error()

            th_master = Thread(target=man.await_notification)
            th_func = Thread(target=func_for_q, args=args, kwargs=kwargs)
            th_func.setDaemon(True)
            th_time = Thread(target=keep_time, args=(check_frequency,))
            th_time.setDaemon(True)

            th_master.start()
            th_func.start()
            th_time.start()
            th_master.join()  # run next line as soon as notified
            if man.yet_returned:
                raise man.raise_overtime_error()
            else:
                return man.get_return_value()

        return wrapper

    return deco


# **********************************
#  Example
# **********************************
@work_time(dt.time(7), dt.time(23))  # seven-eleven
def count_up() -> None:
    i = 0
    while True:
        print(i)
        i += 1
        time.sleep(1)


if __name__ == '__main__':
    print(count_up())